One often hears about Big Data these days: the exponential progression in computing capacity, allowing the processing of unimaginable volumes of data, has empowered both the realms of science and business. This surge has taken the capabilities of computation and data storage to levels that, as we will soon discover, we can manage but find challenging to truly grasp.
We effortlessly navigate through terabytes and gigahertz, and even the renowned computer giant, Google, derives its name from “Googol,” an immense number represented by a 1 followed by a hundred zeros. Nevertheless, can our minds genuinely fathom the vastness of giga, tera, peta, hexa, and other unwieldy magnitudes that evoke comparisons to the improbable wealth of Uncle Scrooge?
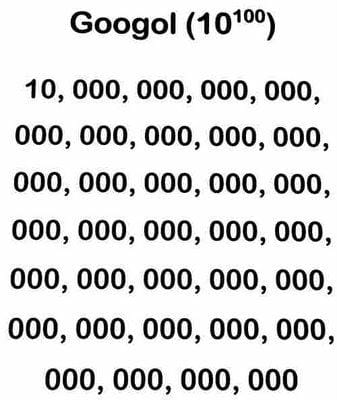
The answer is a resounding no. While our minds can readily grasp quantities that extend into the thousands, the challenge mounts as the figures soar beyond that threshold.
Let’s put this to the test.
Each one of us possesses a personal computer with a hard disk boasting a capacity of no less than one terabyte, equivalent to 10^12 bytes, or one trillion bytes when fully written out.
But let’s delve deeper into its enormity.
Imagine if we were to transcribe each byte residing on our disk onto a strip of paper, each one being 1 cm wide. If we were to lay down these strips end to end, what distance could they span?
The outcome would be a continuous length of paper, akin to a “snake,” capable of circumnavigating the Earth-Moon distance not once, but an astonishing 14 times over.
Alternatively, it could enshroud the Earth’s equatorial circumference more than 784 times.
If each byte were to personify a human being, with 10^12 individuals in tow, we could populate a staggering 142 distinct solar systems, each mirroring our own.
Moreover, imagine for a moment that you found yourself in an extraordinary state of boredom and decided to dedicate your time to transcribing these bytes individually, using nothing but a pen. Astonishingly, the endeavor would consume the same expanse of time it took for the human race to progress from its primal origins to its current state (roughly 32 thousand years). It’s questionable whether, upon reaching the culmination of this feat, you would even entertain the notion of verifying the accuracy of your transcription. The likelihood is that all the ink existing in the world would prove woefully inadequate.
Yet, it’s remarkable to contemplate that this colossal trove of information fits effortlessly within the confines of your jacket pocket. In today’s discourse, the discussion of terabytes fails to provoke any vertigo. Perhaps this resilience to feeling overwhelmed stems from our innate incapability to truly grasp the magnitude of such numbers. It’s akin to observing only a few trees while failing to apprehend the vastness of the entire forest.
MORE INCONCEIVABLE NUMBERS: EXABYTES AND PETABYTES
However, let us now return our focus to the realm of Big Data systems. By definition, these are systems designed to handle data volumes that exceed the capacities of ordinary computers.
Consequently, we’re dealing with quantities surpassing a mere terabyte of information.
Turning our attention to two of the most prominent systems: estimations suggest that Google and YouTube manage an astounding 15 exabytes and 75 petabytes of data, respectively. For reference, an exabyte translates to 10^18 bytes, which is a staggering 1,000,000,000,000,000,000 bytes, if you’d prefer to envision it that way.
Consider this—should Google’s bytes be likened to grains of sand, there would be enough to fill two planets comparable to Earth.
Alternatively, to approach this from a different angle, Google contains roughly 4500 distinct books for each individual inhabiting Earth. Given that each person’s life story could be chronicled in considerably fewer volumes, we can deduce that Google is already equipped to harbor the entirety of any living being’s information, no matter how trivial, spanning from the moment of the Big Bang to the present day.
It’s a notion that can be rather unsettling, isn’t it?
While the volume of information processed by YouTube is unquestionably smaller, it remains boundless in scope.
Should you decide to embark on a quest to watch all of its videos, you would need to dedicate roughly 5700 years of your life to your monitor—an expanse of time eclipsing even the age of the Great Sphinx of Giza.
And if you were to convert all this footage and transfer it to Super 8 film, the resulting tape would stretch across the expanse between Mercury and Venus.
PETABYTE, GOOGOL E GOOGOLPLEX COMPARED
However, an exabyte, and even more so a petabyte, in comparison to a googol, becomes so minuscule that we can confidently treat it as practically zero. Alternatively, from a different perspective, the entire Google archive occupies a mere
0.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000001% of a Googol.
And in a similar vein, a googol pales to insignificance when contrasted with a googolplex: a googolplex is a number represented by 1 followed by a googol (10^100) zeros, or equivalently, 10 googols.
To illustrate this point: no matter how immense a googol may seem, it can be entirely written out in just one or two lines of a standard squared notebook.
In contrast, comprehending the number of digits within a Googolplex is challenging (a Googol itself consists of 101 digits). However, suffice it to say that these digits far surpass the count of elementary particles in the entirety of the observable universe, an estimate that falls within the range of 10^79 to 10^81.
Consequently, while transcribing a googol into decimal notation remains relatively achievable, the same cannot be said for a googolplex. Even if every particle in the universe were converted into paper, ink, or magnetic memory, materializing such an endeavor would prove infeasible.
Assuming, hypothetically, that it was feasible to compile the list of digits constituting a googolplex, even the most formidable contemporary computer would require around 3×10^85 years to accomplish the task. It’s worth noting that the universe has existed for a comparatively modest “1.38*10^10” years.
Furthermore, even within the realm of magnitude, the googolplex evades comparison with other immensely large numbers, such as the Megistone and Graham’s Number. To grasp this distinction, one need only recognize that while the googolplex can be succinctly articulated in exponential notation (like 10^10^100, for instance), a number like Graham’s defies representation within such a framework.
However, we can find solace in the fact that unless we find ourselves within the realms of a technological singularity, the likelihood of encountering these colossal numbers in our everyday lives remains exceedingly slim.



